로지스틱 시그모이드 함수
사이킷런(Sklearn)을 활용하지 않고 로지스틱 회귀 시그모이드 함수 구현하기
기본 설정
- 필수 모듈 불러오기
- 그래프 출력 관련 기본 설정 지정
# 파이썬 ≥3.5 필수
import sys
assert sys.version_info >= (3, 5)
# 사이킷런 ≥0.20 필수
import sklearn
assert sklearn.__version__ >= "0.20"
# 공통 모듈 임포트
import numpy as np
import os
# 노트북 실행 결과를 동일하게 유지하기 위해
np.random.seed(42)
# 깔끔한 그래프 출력을 위해
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# 그림을 저장할 위치
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "training_linear_models"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("그림 저장:", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# 어레이 데이터를 csv 파일로 저장하기
def save_data(fileName, arrayName, header=''):
np.savetxt(fileName, arrayName, delimiter=',', header=header, comments='')
1: 조기 종료 & 배치 경사 하강법 시그모이드 함수(사이킷런 미활용)
조기 종료를 사용한 배치 경사 하강법으로 로지스틱 회귀를 구현하라. 단, 사이킷런을 전혀 사용하지 않아야 한다.
단계 1: 데이터 준비
아래 코드는 이진 분류 설명을 위해 꽃잎 너비(petal width) 특성을 이용하여 버지니카 품종 여부를 판정하는 데에 사용되는 데이터셋을 지정한다.
X = iris["data"][:, (2, 3)] # 꽃잎 길이와 너비
y = (iris["target"] == 2).astype(np.int)
X_with_bias = np.c_[np.ones([len(X), 1]), X]
np.random.seed(1235)
단계 2: 데이터셋 분할
데이터셋을 훈련, 검증, 테스트 용도로 6대 2대 2의 비율로 무작위로 분할한다.
- 훈련 세트: 60%
- 검증 세트: 20%
- 테스트 세트: 20%
아래 코드는 사이킷런의 train_test_split() 함수를 사용하지 않고
수동으로 무작위 분할하는 방법을 보여준다.
먼저 각 세트의 크기를 결정한다.
test_ratio = 0.2 # 테스트 세트 비율 = 20%
validation_ratio = 0.2 # 검증 세트 비율 = 20%
total_size = len(X_with_bias) # 전체 데이터셋 크기
test_size = int(total_size * test_ratio) # 테스트 세트 크기: 전체의 20%
validation_size = int(total_size * validation_ratio) # 검증 세트 크기: 전체의 20%
train_size = total_size - test_size - validation_size # 훈련 세트 크기: 전체의 60%
np.random.permutation() 함수를 이용하여 인덱스를 무작위로 섞는다.
rnd_indices = np.random.permutation(total_size)
인덱스가 무작위로 섞였기 때문에 무작위로 분할하는 효과를 얻는다. 방법은 섞인 인덱스를 이용하여 지정된 6:2:2의 비율로 훈련, 검증, 테스트 세트로 분할하는 것이다.
X_train = X_with_bias[rnd_indices[:train_size]]
y_train = y[rnd_indices[:train_size]]
X_valid = X_with_bias[rnd_indices[train_size:-test_size]]
y_valid = y[rnd_indices[train_size:-test_size]]
X_test = X_with_bias[rnd_indices[-test_size:]]
y_test = y[rnd_indices[-test_size:]]
단계 3: 타깃 변환
타깃은 0, 1로 설정되어 있다. 차례대로 버지니카가 아닌 품종, 버지니카 품종을 가리킨다. 훈련 세트의 첫 5개 샘플의 품종은 다음과 같다.
y_train[:5]
array([0, 0, 0, 0, 1])
학습을 위해 타깃을 원-핫 벡터로 변환해야 한다. 이유는 소프트맥스 회귀는 샘플이 주어지면 각 클래스별로 속할 확률을 구하고 구해진 결과를 실제 확률과 함께 이용하여 비용함수를 계산하기 때문이다.
붓꽃 데이터의 경우 세 개의 품종 클래스별로 속할 확률을 계산해야 하기 때문에 품종을 0, 1의 하나의 숫자로 두기 보다는 해당 클래스는 1, 나머지는 0인 확률값으로 이루어진 어레이로 다루어야 소프트맥스 회귀가 계산한 클래스별 확률과 연결된다.
아래 함수 to_one_hot() 함수는 길이가 m이면서 0, 1로 이루어진 1차원 어레이가 입력되면
(m, 2) 모양의 원-핫 벡터를 반환한다.
def to_one_hot(y):
n_classes = y.max() + 1 # 클래스 수
m = len(y) # 샘플 수
Y_one_hot = np.zeros((m, n_classes)) # (샘플 수, 클래스 수) 0-벡터 생성
Y_one_hot[np.arange(m), y] = 1 # 샘플 별로 해당 클래스의 값만 1로 변경. (넘파이 인덱싱 활용)
return Y_one_hot
샘플 5개에 대해 잘 작동하는 것을 확인할 수 있다.
y_train[:5]
array([0, 0, 0, 0, 1])
to_one_hot(y_train[:5])
array([[1., 0.],
[1., 0.],
[1., 0.],
[1., 0.],
[0., 1.]])
이제 훈련/검증/테스트 세트의 타깃을 모두 원-핫 벡터로 변환한다.
Y_train_one_hot = to_one_hot(y_train)
Y_valid_one_hot = to_one_hot(y_valid)
Y_test_one_hot = to_one_hot(y_test)
단계 4: 로지스틱 회귀 시그모이드 함수
def sigmoid(logits):
return 1.0 / (1 + np.exp(-logits)) # 시그모이드 함수 구현
단계 5: 경사하강법 활용 훈련
경사하강법을 구현하기 위해 아래 비용함수와 비용함수의 그레이디언트를 파이썬으로 구현할 수 있어야 한다.
- 비용 함수($K$는 클래스 수, $m$은 샘플 수):
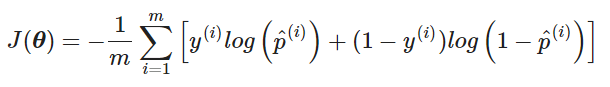
위의 수식을 코드로 표현하면 다음과 같다.
-np.mean(np.sum((y_trainnp.log(Y_proba + epsilon) + (1-y_train)np.log(1 - Y_proba + epsilon))))
- 그레이디언트 공식(클래스 k에 대해):
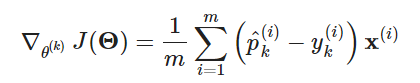
이제 훈련 코드를 작성할 수 있다. 클래스별 파라미터로 이루어진 (n+1, K) 행렬 모양의 2차원 넘파이 어레이 Θ를 생성하기 위해 n과 K를 확인한다.
n_inputs = X_train.shape[1] # 특성 수(n) + 1, 붓꽃의 경우: 특성 2개 + 1
n_outputs = len(np.unique(y_train)) # 중복을 제거한 클래스 수(K), 붓꽃의 경우: 3개
파라미터 Θ를 무작위로 초기 설정한다.
Theta = np.random.randn(n_inputs, n_outputs)
배치 경사하강법 훈련은 아래 코드를 통해 이루어진다.
eta = 0.01: 학습률n_iterations = 5001: 에포크 수m = len(X_train): 훈련 세트 크기, 즉 훈련 샘플 수epsilon = 1e-7: log 값이 항상 계산되도록 더해지는 작은 실수logits: 모든 샘플에 대한 클래스별 점수Y_proba: 모든 샘플에 대해 계산된 클래스 별 소속 확률
# 배치 경사하강법 구현
eta = 0.1
n_iterations = 20001
m = len(X_train)
epsilon = 1e-7
Theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations): # 20001번 반복 훈련
logits = X_train.dot(Theta)
Y_proba = sigmoid(logits)
if iteration % 1000 == 0: # 1000 에포크마다 손실(비용) 계산해서 출력
loss = -np.mean(np.sum((Y_train_one_hot*np.log(Y_proba + epsilon) + (1-Y_train_one_hot)*np.log(1 - Y_proba + epsilon))))
print(iteration, loss)
error = Y_proba - Y_train_one_hot # 그레이디언트 계산.
gradients = 1/m * X_train.T.dot(error)
Theta = Theta - eta * gradients # 파라미터 업데이트
0 424.17283178098626
1000 41.043384218852445
2000 32.74074062063721
3000 28.744312224357305
4000 26.237295992550052
5000 24.474139687325014
6000 23.150000374030935
7000 22.11153790859484
8000 21.271448179525667
9000 20.57570343517272
10000 19.988786219677582
11000 19.486246358338462
12000 19.0506272909059
13000 18.669090438381183
14000 18.33195790344411
15000 18.03178070374586
16000 17.762722037185707
17000 17.52013688117732
18000 17.300278070184774
19000 17.100086212554693
20000 16.91703658618475
학습된 파라미터는 다음과 같다.
Theta
array([[ 17.42973906, -17.40609421],
[ -1.21742315, 1.20856212],
[ -6.93030596, 6.94259264]])
검증 세트에 대한 예측과 정확도는 다음과 같다.
logits, Y_proba를 검증 세트인 X_valid를 이용하여 계산한다.
예측 클래스는 Y_proba에서 가장 큰 값을 갖는 인덱스로 선택한다.
logits = X_valid.dot(Theta)
Y_proba = sigmoid(logits)
y_predict = np.argmax(Y_proba, axis=1) # 가장 높은 확률을 갖는 클래스 선택
accuracy_score = np.mean(y_predict == y_valid) # 정확도 계산
accuracy_score
0.9333333333333333
단계 6: 규제가 추가된 경사하강법 활용 훈련
ℓ2 규제가 추가된 경사하강법 훈련을 구현한다.
코드는 기본적으로 동일하다.
다만 손실(비용)에 ℓ2 페널티가 추가되었고
그래디언트에도 항이 추가되었다(Theta의 첫 번째 원소는 편향이므로 규제하지 않습니다).
- 학습률
eta증가됨. alpha = 0.2: 규제 강도
eta = 0.1
n_iterations = 20001
m = len(X_train)
epsilon = 1e-7
alpha = 0.2 # 규제 하이퍼파라미터
Theta = np.random.randn(n_inputs, n_outputs) # 파라미터 새로 초기화
for iteration in range(n_iterations):
logits = X_train.dot(Theta)
Y_proba = sigmoid(logits)
if iteration % 1000 == 0:
xentropy_loss = -np.mean(np.sum((Y_train_one_hot*np.log(Y_proba + epsilon) + (1-Y_train_one_hot)*np.log(1 - Y_proba + epsilon))))
l2_loss = 1/2 * np.sum(np.square(Theta[1:])) # 편향은 규제에서 제외
loss = xentropy_loss + alpha * l2_loss # l2 규제가 추가된 손실
print(iteration, loss)
error = Y_proba - Y_train_one_hot
l2_loss_gradients = np.r_[np.zeros([1, n_outputs]), alpha * Theta[1:]] # l2 규제 그레이디언트
gradients = 1/m * X_train.T.dot(error) + l2_loss_gradients
Theta = Theta - eta * gradients
0 487.6838219479042
1000 56.90670055992519
2000 54.189604938235796
3000 53.70682558231622
4000 53.609377773456686
5000 53.58923113138052
6000 53.58504554936091
7000 53.58417508939525
8000 53.58399402496207
9000 53.5839563600891
10000 53.58394852500216
11000 53.58394689513592
12000 53.58394655608864
13000 53.58394648555954
14000 53.58394647088794
15000 53.58394646783594
16000 53.58394646720106
17000 53.58394646706902
18000 53.58394646704159
19000 53.583946467035844
20000 53.583946467035844
Theta
array([[ 4.62124922, -4.62124922],
[-0.78010499, 0.78010499],
[-0.44256214, 0.44256214]])
logits = X_valid.dot(Theta)
Y_proba = sigmoid(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
0.9666666666666667
단계 7: 조기 종료 추가
위 규제가 사용된 모델의 훈련 과정에서 매 에포크마다 검증 세트에 대한 손실을 계산하여 오차가 줄어들다가 증가하기 시작할 때 멈추도록 한다.
eta = 0.1
n_iterations = 20001
m = len(X_train)
epsilon = 1e-7
alpha = 0.2 # 규제 하이퍼파라미터
best_loss = np.infty # 최소 손실값 기억 변수
Theta = np.random.randn(n_inputs, n_outputs) # 파라미터 새로 초기화
for iteration in range(n_iterations):
# 훈련 및 손실 계산
logits = X_train.dot(Theta)
Y_proba = sigmoid(logits)
error = Y_proba - Y_train_one_hot
gradients = 1/m * X_train.T.dot(error) + np.r_[np.zeros([1, n_outputs]), alpha * Theta[1:]]
Theta = Theta - eta * gradients
# 검증 세트에 대한 손실 계산
logits = X_valid.dot(Theta)
Y_proba = sigmoid(logits)
xentropy_loss = -np.mean(np.sum((Y_valid_one_hot*np.log(Y_proba + epsilon) + (1-Y_valid_one_hot)*np.log(1 - Y_proba + epsilon))))
l2_loss = 1/2 * np.sum(np.square(Theta[1:]))
loss = xentropy_loss + alpha * l2_loss
# 1000 에포크마다 검증 세트에 대한 손실 출력
if iteration % 1000 == 0:
print(iteration, loss)
# 에포크마다 최소 손실값 업데이트
if loss < best_loss:
best_loss = loss
else: # 에포크가 줄어들지 않으면 바로 훈련 종료
print(iteration - 1, best_loss) # 종료되지 이전 에포크의 손실값 출력
print(iteration, loss, "조기 종료!")
break
0 158.16482495414078
1000 21.78277529179991
2000 20.85194273875507
3000 20.68742353724357
4000 20.65424689662067
5000 20.64738916739576
6000 20.645964490415082
7000 20.645668208054406
8000 20.64560657844655
9000 20.645593758311257
10000 20.64559109145327
11000 20.645590536689596
12000 20.645590421286787
13000 20.64559039728052
14000 20.645590392286696
15000 20.64559039124788
16000 20.64559039103179
17000 20.645590390986843
17332 20.645590390982044
17333 20.645590390982044 조기 종료!
Theta
array([[ 4.62124922, -4.62124922],
[-0.78010499, 0.78010499],
[-0.44256214, 0.44256214]])
logits = X_valid.dot(Theta)
Y_proba = sigmoid(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
0.9666666666666667
예측 값이 처음에는 0.93에서 규제와 조기종료가 포함되고서 0.96으로 올라갔다.
사실 시드 값에 따라 올라갔다가 떨어지다가 랜덤이지만, 데이터 값이 적어서 그런 것이라고 판단된다.
연습 2: 연습 1 + 다중 클래스 분류
1에서 구현된 로지스틱 회귀 알고리즘에 일대다(OvR) 방식을 적용하여 붓꽃에 대한 다중 클래스 분류 알고리즘을 구현하라. 단, 사이킷런을 전혀 사용하지 않아야 한다.
np.random.seed(2042)
데이터 전처리 def 정의
def datasetting(X, y):
X_with_bias = np.c_[np.ones([len(X), 1]), X]
test_ratio = 0.2 # 테스트 세트 비율 = 20%
validation_ratio = 0.2 # 검증 세트 비율 = 20%
total_size = len(X_with_bias) # 전체 데이터셋 크기
test_size = int(total_size * test_ratio) # 테스트 세트 크기: 전체의 20%
validation_size = int(total_size * validation_ratio) # 검증 세트 크기: 전체의 20%
train_size = total_size - test_size - validation_size # 훈련 세트 크기: 전체의 60%
rnd_indices = np.random.permutation(total_size)
X_train = X_with_bias[rnd_indices[:train_size]]
y_train = y[rnd_indices[:train_size]]
X_valid = X_with_bias[rnd_indices[train_size:-test_size]]
y_valid = y[rnd_indices[train_size:-test_size]]
X_test = X_with_bias[rnd_indices[-test_size:]]
y_test = y[rnd_indices[-test_size:]]
Y_train_one_hot = to_one_hot(y_train)
Y_valid_one_hot = to_one_hot(y_valid)
Y_test_one_hot = to_one_hot(y_test)
return X_train, y_train, X_valid, y_valid, X_test, y_test, Y_train_one_hot, Y_valid_one_hot, Y_test_one_hot
iris 데이터셋(붓꽃 데이터)가 50 단위로 나뉘는데, 각각 품종에 따른 Theta값 구하기
i = 0
a = 50
b = []
while i < 150:
X = iris["data"][i:a][:, (2, 3)] # 꽃잎 길이와 너비
y = iris["target"][i:a]
datasetting(X, y)
n_inputs = X_train.shape[1] # 특성 수(n) + 1, 붓꽃의 경우: 특성 2개 + 1
n_outputs = len(np.unique(y_train)) # 중복을 제거한 클래스 수(K), 붓꽃의 경우: 3개
Theta = np.random.randn(n_inputs, n_outputs)
eta = 0.1
n_iterations = 20001
m = len(X_train)
epsilon = 1e-7
alpha = 0.2 # 규제 하이퍼파라미터
best_loss = np.infty # 최소 손실값 기억 변수
Theta = np.random.randn(n_inputs, n_outputs) # 파라미터 새로 초기화
for iteration in range(n_iterations):
# 훈련 및 손실 계산
logits = X_train.dot(Theta)
Y_proba = sigmoid(logits)
error = Y_proba - Y_train_one_hot
gradients = 1/m * X_train.T.dot(error) + np.r_[np.zeros([1, n_outputs]), alpha * Theta[1:]]
Theta = Theta - eta * gradients
# 검증 세트에 대한 손실 계산
logits = X_valid.dot(Theta)
Y_proba = sigmoid(logits)
xentropy_loss = -np.mean(np.sum((Y_valid_one_hot*np.log(Y_proba + epsilon) + (1-Y_valid_one_hot)*np.log(1 - Y_proba + epsilon))))
l2_loss = 1/2 * np.sum(np.square(Theta[1:]))
loss = xentropy_loss + alpha * l2_loss
# 1000 에포크마다 검증 세트에 대한 손실 출력
if iteration % 1000 == 0:
print(iteration, loss)
# 에포크마다 최소 손실값 업데이트
if loss < best_loss:
best_loss = loss
else: # 에포크가 줄어들지 않으면 바로 훈련 종료
print(iteration - 1, best_loss) # 종료되지 이전 에포크의 손실값 출력
print(iteration, loss, "조기 종료!")
break
i += 50
a += 50
b.append(Theta)
0 70.66529783165817
5 42.16963510195836
6 42.21402352002106 조기 종료!
0 39.746341342289384
1000 21.585289185618613
2000 20.819933833361397
3000 20.68107137089968
4000 20.652938156954345
5000 20.647117463396086
6000 20.645907993535097
7000 20.645656456497843
8000 20.645604133913228
9000 20.64559324979751
10000 20.64559098567153
11000 20.64559051468471
12000 20.645590416709297
13000 20.645590396328316
14000 20.645590392088625
15000 20.64559039120667
16000 20.64559039102322
17000 20.645590390985063
17442 20.645590390980036
17443 20.645590390980036 조기 종료!
0 238.9134259054118
1000 21.7939936121296
2000 20.853767525221155
3000 20.687785823055552
4000 20.654321544543702
5000 20.647404665108493
6000 20.6459677129491
7000 20.64566887835367
8000 20.64560671788077
9000 20.64559378731647
10000 20.645591097486967
11000 20.645590537944727
12000 20.64559042154789
13000 20.645590397334846
14000 20.645590392298008
15000 20.645590391250217
16000 20.64559039103228
17000 20.645590390986946
17452 20.6455903909809
17453 20.6455903909809 조기 종료!
Theta 값들을 비교하여 best Theta 값 찾기
i = 0
best_Y_proba = []
while i < 3:
logits = X_valid.dot(b[i])
Y_proba = sigmoid(logits)
best_Y_proba.append(Y_proba)
i+=1
w1 = best_Y_proba[0]
w2 = best_Y_proba[1]
w3 = best_Y_proba[2]
i = 0
w4 = np.zeros((30, 2))
while i < len(w1):
if w1[i,0] > w2[i,0]:
w4[i,0] = w1[i,0]
else:
w4[i,0] = w2[i,0]
if w3[i,0] > w4[i,0]:
w4[i,0] = w3[i,0]
if w1[i,1] > w2[i,1]:
w4[i,1] = w1[i,1]
else:
w4[i,1] = w2[i,1]
if w3[i,1] > w4[i,1]:
w4[i,1] = w3[i,1]
i+=1
w4
array([[0.44549037, 0.59071592],
[0.4843735 , 0.52999988],
[0.47373974, 0.72676269],
[0.97331512, 0.45092582],
[0.96352836, 0.46241888],
[0.96651435, 0.4429628 ],
[0.96894927, 0.44561409],
[0.72715913, 0.45160281],
[0.52002264, 0.51119426],
[0.60990991, 0.48979979],
[0.51184044, 0.69200036],
[0.49471783, 0.50528217],
[0.51365403, 0.77622417],
[0.46807052, 0.70182271],
[0.57221952, 0.48443415],
[0.49187243, 0.66300607],
[0.60184996, 0.47731212],
[0.95579855, 0.46684456],
[0.60990991, 0.48979979],
[0.74034552, 0.47647189],
[0.47675975, 0.53839877],
[0.51752401, 0.71743112],
[0.5146217 , 0.76238249],
[0.48219483, 0.81104647],
[0.83262417, 0.47295427],
[0.48340606, 0.54937712],
[0.96505208, 0.45267276],
[0.96758975, 0.45533467],
[0.65874639, 0.46309857],
[0.66395405, 0.49785228]])
가장 좋은 성능을 보이는 Theta 값을 찾음
y_predict = np.argmax(w4, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
0.9666666666666667