텐서 플로우(TensorFlow) - 1
1. 텐서 소개
#1 TensorFlow import
import tensorflow as tf
import numpy as np
지원되는 모든 dtypes은 tf.dtypes.DType에서 볼 수 있다.
텐서는 일종의 np.arrays와 같다.
#2 TensorFlow DType Check
tf.dtypes.DType
모든 텐서는 Python 숫자 및 문자열과 같이 변경할 수 없다.
텐서의 내용은 업데이트할 수 없고, 새로운 텐서를 생성할 수만 있다.
1.1. 즉시 실행(Eager execution)
텐서플로의 즉시 실행(Eager execution)은 그래프를 생성하지 않고 함수를 바로 실행하는 명령형 프로그래밍 환경이다.
나중에 실행하기 위해 계산가능한 그래프를 생성하는 대신에 계산 값을 즉시 알려주는 연산이다.
이러한 기능은 텐서플로를 시작하고 모델을 디버깅하는 것을 더욱 쉽게 만들고 불필요한 상용구 코드(boilerplate code) 작성을 줄인다.
즉시 실행(Eager execution)은 연구와 실험을 위한 유연한 기계학습 플랫폼으로 다음과 같은 기능을 제공힌다:
-
직관적인 인터페이스-코드를 자연스럽게 구조화하고 파이썬의 데이터 구조를 활용. 작은 모델과 작은 데이터를 빠르게 반복
-
손쉬운 디버깅-실행중인 모델을 검토하거나 변경 사항을 테스트해보기 위해서 연산을 직접 호출. 에러 확인을 위해서 표준 파이썬 디버깅 툴을 사용
-
자연스런 흐름 제어-그래프 제어 흐름 대신에 파이썬 제어 흐름을 사용함으로써 동적인 모델 구조의 단순화
즉시 실행(Eager execution)은 대부분의 텐서플로 연산과 GPU 가속을 지원한다.
2. 기본 텐서
기본 텐서를 알아보자.
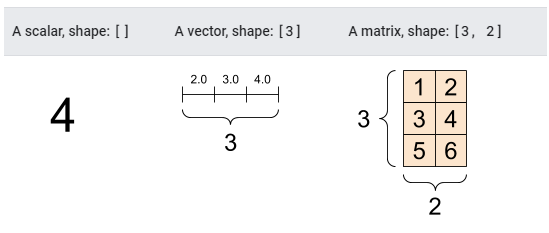
2.1. “스칼라(Scalar)” or “순위-0(rank-0)” Tensor
- 스칼라는 단일 값을 포함하며 “축”은 없다.
#3 기본적으로 int32 텐서가 된다. 아래 유형 참조
rank_0_tensor = tf.constant(4)
print(rank_0_tensor)
tf.Tensor(4, shape=(), dtype=int32)
2.2. “벡터(Vector)” or “순위-1(rank-1)” Tensor
- 벡터 텐서는 값의 목록과 같다.
- 벡터에는 하나의 축이 있다.
#4 벡터를 이용해 float 텐서를 만들어 보자.
rank_1_tensor = tf.constant([2.0, 3.0, 4.0])
print(rank_1_tensor)
tf.Tensor([2. 3. 4.], shape=(3,), dtype=float32)
2.3. “행렬(matrix)” or “순위-2(rank-2)” Tensor
- 행렬에는 두 개의 축이 있다.
#5 구체적으로 설명하려면 생성 시 dtype을 설정할 수 있다.
rank_2_tensor = tf.constant([[1, 2],
[3, 4],
[5, 6]], dtype=tf.float16)
print(rank_2_tensor)
텐서에는 더 많은 축이 있을 수 있고 여기선 세 개의 축이 있는 텐서가 사용된다.
#6 임의의 숫자가 있을 수 있다.
# 축(차원)이라고도 함.
rank_3_tensor = tf.constant([
[[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]],
[[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]],])
print(rank_3_tensor)
tf.Tensor(
[[[ 0 1 2 3 4]
[ 5 6 7 8 9]]
[[10 11 12 13 14]
[15 16 17 18 19]]
[[20 21 22 23 24]
[25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
3. 텐서(Tensor)의 시각화
축이 두 개 이상인 텐서를 시각화하는 방법에는 여러 가지가 있다.
![A 3-axis tensor, shape: [3, 2, 5]](/images/tensor2.png)
np.array 또는 tensor.numpy 메서드를 사용하여 텐서를 NumPy 배열로 변환할 수 있다.
#7 np.array 이용 방법
np.array(rank_2_tensor)
array([[1., 2.],
[3., 4.],
[5., 6.]], dtype=float16)
#8 tensor.numpy 이용 방법
rank_2_tensor.numpy()
array([[1., 2.],
[3., 4.],
[5., 6.]], dtype=float16)
텐서에는 float와 int의 유형이지만 다음과 같은 다른 유형도 존재한다.
- 복소수
- 문자열
기본 tf.Tensor 클래스에서는 텐서가 “직사각형”이어야 한다.
즉, 각 축을 따라 모든 요소의 크기가 같다.
그러나 다양한 형상을 처리할 수 있는 특수 유형의 텐서가 존재한다.
- 비정형
- 희소
이 유형은 덧셈, 요소별 곱셈 및 행렬 곱셈을 포함하여 텐서에 대한 기본 산술을 수행할 수 있다.
#9 Could have also said `tf.ones([2,2])`
a = tf.constant([[1, 2],
[3, 4]])
b = tf.constant([[1, 1],
[1, 1]])
print(tf.add(a, b), "\n")
print(tf.multiply(a, b), "\n")
print(tf.matmul(a, b), "\n")
tf.Tensor(
[[2 3]
[4 5]], shape=(2, 2), dtype=int32)
tf.Tensor(
[[1 2]
[3 4]], shape=(2, 2), dtype=int32)
tf.Tensor(
[[3 3]
[7 7]], shape=(2, 2), dtype=int32)
텐서는 모든 종류의 연산(ops)에 사용된다.
c = tf.constant([[4.0, 5.0], [10.0, 1.0]])
#10 가장 큰 값 찾기
print(tf.reduce_max(c))
# 가장 큰 인덱스 찾기
print(tf.argmax(c))
# 소프트맥스 계산
print(tf.nn.softmax(c))
tf.Tensor(10.0, shape=(), dtype=float32)
tf.Tensor([1 0], shape=(2,), dtype=int64)
tf.Tensor(
[[2.6894143e-01 7.3105854e-01]
[9.9987662e-01 1.2339458e-04]], shape=(2, 2), dtype=float32)
4. 형상 정보(About shapes)
텐서에는 형상이 있다.
사용되는 일부 용어는 다음과 같다.
- 형상: 텐서의 각 차원의 길이(요소의 수)
- 순위: 텐서 축의 수. 스칼라는 순위가 0이고 벡터의 순위는 1이며 행렬의 순위는 2이다.
- 축(차원): 텐서의 특정 차원
- 크기: 텐서의 총 항목 수, 곱 형상 벡터
참고: “2차원 텐서”에 대한 참조가 있을 수 있지만, 순위-2 텐서는 일반적으로 2D 공간을 설명하지 않는다.
텐서 및 tf.TensorShape 객체에는 다음에 액세스하기 위한 편리한 속성이 있다.
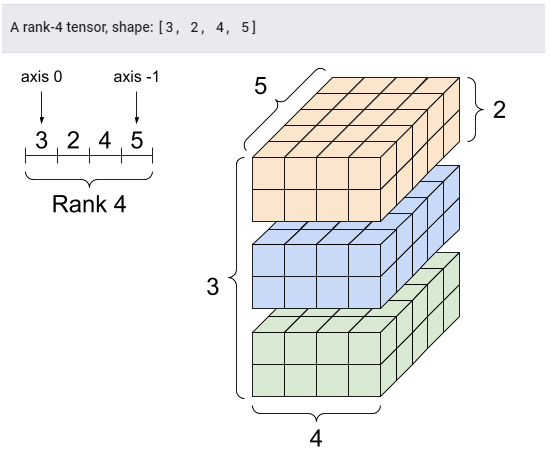
#11
rank_4_tensor = tf.zeros([3, 2, 4, 5])
print("Type of every element:", rank_4_tensor.dtype)
print("Number of dimensions:", rank_4_tensor.ndim)
print("Shape of tensor:", rank_4_tensor.shape)
print("Elements along axis 0 of tensor:", rank_4_tensor.shape[0])
print("Elements along the last axis of tensor:", rank_4_tensor.shape[-1])
print("Total number of elements (3*2*4*5): ", tf.size(rank_4_tensor).numpy())
Type of every element: <dtype: 'float32'>
Number of dimensions: 4
Shape of tensor: (3, 2, 4, 5)
Elements along axis 0 of tensor: 3
Elements along the last axis of tensor: 5
Total number of elements (3*2*4*5): 120
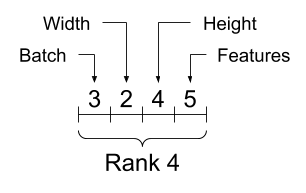
축은 인덱스로 참조하지만, 항상 각 축의 의미를 추적해야 한다.
축이 전역에서 로컬로 정렬되는 경우가 있는데, 배치 축이 먼저 오고 그 다음에 공간 차원과 각 위치의 특성이 마지막에 온다.
5. 인덱싱(Indexing)
5.1. 단일 축 인덱싱(Single-axis indexing)
TensorFlow는 파이썬의 목록 또는 문자열 인덱싱과 마찬가지로 표준 파이썬 인덱싱 규칙과 numpy 인덱싱의 기본 규칙을 따른다.
`
- 인덱스는
0부터 시작 - 음수 인덱스는 끝에서부터 거꾸로 계산
- 콜론,
:은 슬라이스start:stop:step에 사용
#12
rank_1_tensor = tf.constant([0, 1, 1, 2, 3, 5, 8, 13, 21, 34])
print(rank_1_tensor.numpy())
[ 0 1 1 2 3 5 8 13 21 34]
스칼라를 사용하여 인덱싱하면 축이 제거된다.
#13
print("First:", rank_1_tensor[0].numpy())
print("Second:", rank_1_tensor[1].numpy())
print("Last:", rank_1_tensor[-1].numpy())
First: 0
Second: 1
Last: 34
: 슬라이스를 사용하여 인덱싱하면 축이 유지된다.
#14
print("Everything:", rank_1_tensor[:].numpy())
print("Before 4:", rank_1_tensor[:4].numpy())
print("From 4 to the end:", rank_1_tensor[4:].numpy())
print("From 2, before 7:", rank_1_tensor[2:7].numpy())
print("Every other item:", rank_1_tensor[::2].numpy())
print("Reversed:", rank_1_tensor[::-1].numpy())
Everything: [ 0 1 1 2 3 5 8 13 21 34]
Before 4: [0 1 1 2]
From 4 to the end: [ 3 5 8 13 21 34]
From 2, before 7: [1 2 3 5 8]
Every other item: [ 0 1 3 8 21]
Reversed: [34 21 13 8 5 3 2 1 1 0]
5.2. 다축 인덱싱(Multi-axis indexing)
더 높은 순위의 텐서는 여러 인덱스를 전달하여 인덱싱된다.
단일 축의 경우에서와 정확히 같은 규칙이 각 축에 독립적으로 적용됨.
#15
print(rank_2_tensor.numpy())
[[1. 2.]
[3. 4.]
[5. 6.]]
각 인덱스에 정수를 전달하면 결과는 스칼라다.
#16 2순위 텐서에서 단일 값을 추출
print(rank_2_tensor[1, 1].numpy())
4.0
정수와 슬라이스를 조합하여 인덱싱할 수 있다.
#17 행 및 열 텐서 가져오기
print("Second row:", rank_2_tensor[1, :].numpy())
print("Second column:", rank_2_tensor[:, 1].numpy())
print("Last row:", rank_2_tensor[-1, :].numpy())
print("First item in last column:", rank_2_tensor[0, -1].numpy())
print("Skip the first row:")
print(rank_2_tensor[1:, :].numpy(), "\n")
Second row: [3. 4.]
Second column: [2. 4. 6.]
Last row: [5. 6.]
First item in last column: 2.0
Skip the first row:
[[3. 4.]
[5. 6.]]
여기까지 마지막으로 다축 인덱싱 알아 보았고, 내용이 많아 글을 나눠서 쓰려고 한다.
이미지 출처: (https://www.tensorflow.org/guide/tensor/)